Introduzione alle telecomunicazioni

telecomunicazione = comunicare informazioni a distanza

comunicare = trasferire informazioni tra pi?punti =>

monodirezionale (telemetria F1); bidirezionale (telefoni)

tra due interlocutori (telefoni); tra molti interlocutori (radiodiffusione) =>

da uno ai tanti (televisione); tra tanti in contemporanea (teleconferenza)

informazione = tutto ci?che intendiamo trasmettere

sistemi di telecomunicazioni = dispositivi e funzioni correlate impiegati per trasferire tra due o pi?punti le informazioni

 

dispositivi attuali: elettricita' in tutte le sue forme

 

 

schema di un sistema di telecomunicazioni:

 

 

 

 

 

informazione = segnale (codice; voce; suono; immagine; dati)

 

 

 

 

 

 

 

Trasduttori = dispositivi atti a trasformare l'informazione in segnali elettrici (tasto telegrafico; microfono; telecamera; tastiera computer)

Terminale di trasmissione = apparecchi impiegati per adattare il segnale al mezzo trasmissivo (amplificatori; filtri; modulatori; multi-plexer; antenne)

Mezzo trasmissivo = strada su cui viaggiano i segnali (cavi; etere; fibra ottica)

Disturbo = segnale pi?o meno casuale che interferisce con la comunicazione (scarica elettrostatica; rumore elettronico; rumore fisico; interferenza tra collegamenti diversi)

Terminale di ricezione = apparato per captare ed elaborare il debole segnale ricevuto (amplificatori; filtri; demodulatori; demultiplexer; antenne)

Trasduttore = ripristina l'informazione (con una piccola componente di disturbo)

 

 

Il segnale

 

Segnale analogico = nell'intervallo di tempo la grandezza elettrica pu?assumere tutti gli infiniti valori con continuit?(una temperatura; una tele-fonata; ecc...)

 

 

 

 

 

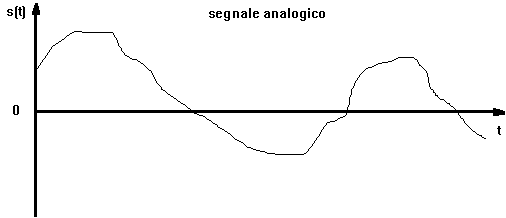
(anche un segnale tempo discreto se pu?assumere infiniti valori nelle ampiezze ?analogico).

 

Segnale discreto = nel tempo le grandezze elettriche assumono solo distinti valori (interruttore on-off; dati numerici; luce intermittente)

 

 

 

 

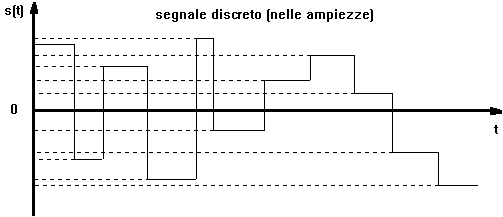
il segnale discreto ?anche detto digitale (dall'inglese digit cio?dito)

il segnale tempo-discreto pi?utilizzato ?quello composto da due soli stati (ad esempio 1 e 0 oppure 1 e -1) che prende il nome di binario ed il singolo impulso viene indicato con il termine BIT (cio? BInary digiT)

 

 

 

 

 

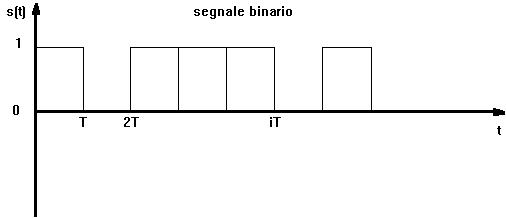
segnale misto = l'insieme dei segnali analogici e digitali (immagine TV)

 

 

Classificazione dei segnali

segnale periodico = quando ad ogni intervallo di tempo T (periodo) l'andamento del segnale si ripete perfettamente. Il numero di volte che il periodo si ripete nell'unit?di tempo si chiama frequenza: il legame tra periodo e frequenza ?di tipo inverso; cio?

 

 

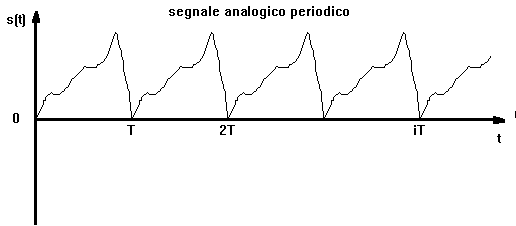
segnale non periodico = il segnale ha una forma d'onda qualsiasi

segnale alternativo (periodico o no) = quando la grandezza elettrica assume alternativamente valori positivi e negativi

segnale impulsivo (periodico o no) = il segnale assume solo valori di un unico segno

il segnale pu?essere visto nel dominio del tempo o della frequenza: punti di vista differenti dello stesso fenomeno

 

l'andamento nei tempi del segnale si chiama forma d'onda; mentre nelle frequenze si chiame spettro

parliamo di durata temporale quando consideriamo quei tempi per i quali il segnale ha un valore apprezzabile; e di banda del segnale quando consideriamo l'insieme delle frequenze che compongono lo spettro del segnale.

 

 

 

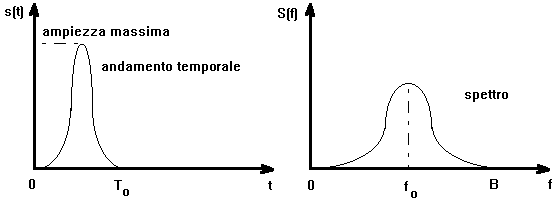
Genesi del legame matematico tra dominio T

e dominio F: la serie di Fourier

 

 

L'elemento base della scomposizione di Fourier ?la sinusoide: ad ogni sinusoide di frequenza f0 ed ampiezza A nei tempi corrisponde una "barra" di banda infinitesima ed ampiezza A alla frequenza f0 nelle frequenze

 

 

 

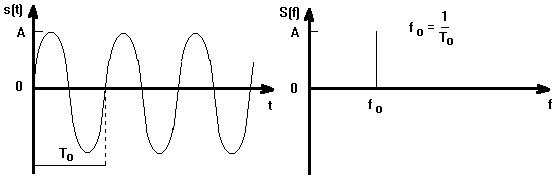
Il teorema di Fourier ci assicura che:

Tutti i segnali s(t) periodici fisicamente realizzabili possono essere sviluppati nella serie:

 

con s(t) segnale periodico;

w0 = 2p f0 pulsazione;

f0 = 1/T frequenza fondamentale (inverso del periodo);

A0 = valor medio di s(t) o componente continua del segnale;

An Bn = coefficienti della serie di Fourier;

Cn = coefficienti complessi di Fourier abbinati alle sinusoidi complesse

 

se s(t) ?pari allora Bn = 0; se S(t) ?dispari allora An =0

se n ?pari parliamo di armoniche pari mentre se n ?dispari parliamo di armoniche dispari

per n = 1 armonica fondamentale (componente a frequenza 1/T)

per n > 1 armoniche (seconda; terza; ecc...)

siccome una sinusoide nei tempi ?una barra nelle frequenze allora una somma di sinusoidi nei tempi ?una sovrapposizione di barre nelle frequenze per cui un segnale periodico nei tempi ha uno spettro composto da un insieme di barre.

 

 

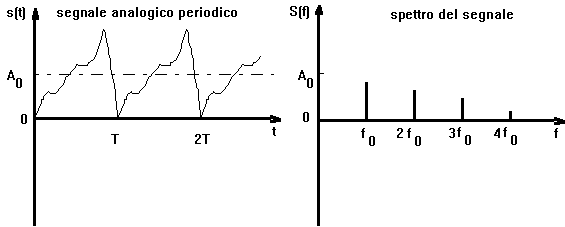
il significato del teorema ?che ?possibile decomporre un segnale periodico in somma di tutte le sue armoniche.

Questo tipo di segnale ?tipico dei suoni dove la fondamentale determina l'altezza della nota, e la composizione armonica, (cio?l'insieme delle frequenze superiori), determinano il timbro

Si pu?osservare che spesso al segnale corrispondono infinite armoniche la cui importanza tende a decrescere con il crescere della frequenza, quindi fissata una soglia si pu?definire una banda utile dello spettro del segnale

 

 

 

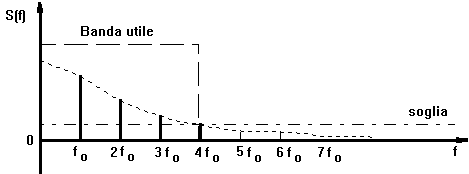
Allora utilizzando solo le armoniche pi?importanti ? possibile ricostruire il segnale con una accettabile fedelt? inoltre tanto pi? il segnale nei tempi varier?bruscamente tanto pi?alte saranno le armoniche da non trascurare, per cui tanto pi?alta sar?la banda utile del segnale

 

L'operazione di taglio di alcune componenti in frequenza si chiama filtraggio

 

 

Estensione del teorema di Fourier ad i segnali non periodici

 

Se T tende all'infinito la distanza tra le armoniche tende a zero, cio?un segnale s(t) qualunque pu?essere scomposto in infinite sinusoidi infinitamente vicine. Si ottiene allora la trasformata di Fourier che d? il legame tra il dominio dei tempi con quello delle frequenze.

 

 

 

 

 

 

s(t) continuo non periodico <=> S(f) continuo non periodico

s(t) periodico <=> S(f) discreto nelle frequenze

s(t) tempo discreto <=> S(f) continuo e periodico

 

Anche ora notiamo che a segnali che hanno durate temporali grandi corrispondono spettri con banda stretta e viceversa

 

 

conoscere la banda di un segnale ?importante perch?ci permette di stabilire:

le caratteristiche che deve avare il mezzo trasmissivo

la lunghezza della tratta

la distorsione accettabile

la quantit?di informazione trasferibile

 

le operazioni che verranno compiute sul segnale sono principalmente:

selezione di banda

 

 

 

 

 

 

 

 

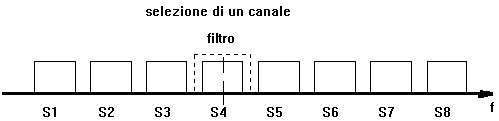
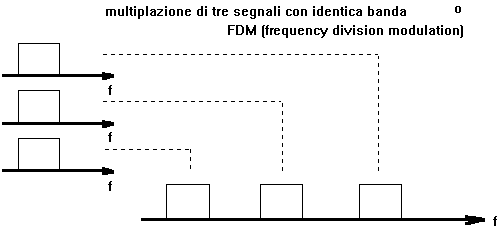
multiplazione di pi?segnali

 

 

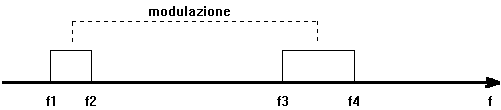
modulazione del segnale

 

 

 

Il rumore

 

Le prestazioni di un sistema di telecomunicazione sono subordinate al rumore misurato in ricezione.

 

 

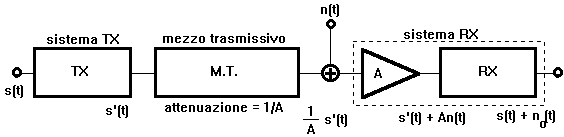
Il rumore ?un segnale indesiderato che si sovrappone alla comunicazione

 

 

cause del rumore:

agitazione caotica degli elettroni a temperatura ambiente

imperfezioni nei materiali costituenti il sistema di telecomunicazione

tipi di rumore:

rumore termico, (Johnson) = moto caotico delle particelle "calde"

intermodulazione = interferenze tra canali adiacenti per non linearit?dei sistemi

scariche elettriche = disturbi di fenomeni naturale (meteo)

induzione elettromagnetica tra conduttori = i conduttori non schermati sono come antenne

transitori di commutazione = scariche elettriche di natura "umana"

residui nell'alimentazione = ripple e sovraccarichi della rete di alimentazione

si possono riassumere come:

disturbi di fondo (rumore bianco)

disturbi impulsivi (con banda definita)

 

 

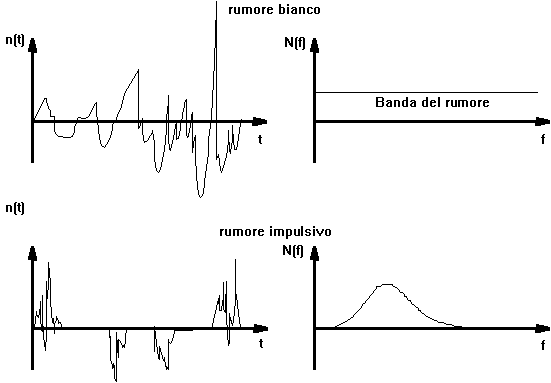
In tutti i casi parte del rumore si sovrappone alla banda del segnale e pu?essere eliminata solo quella componente che filtrata non giace nella banda del segnale

 

 

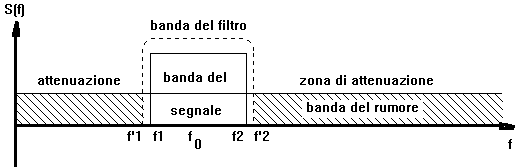
Il parametro che stabilisce la qualit?del sistema ?il rapporto segnale-rumore SNR che dichiara la potenza del segnale riferita a quella del rumore nella banda del segnale, (questo termine ?spesso espresso in dB), il CCITT attraverso le raccomandazioni M.1020, e M.1025 specifica le modalit?di misura del rapporto SNR

 

(se il segnale ?facilmente trattabile con i termini matematici dell'elettrotecnica il rumore, essendo un fenomeno casuale, deve essere trattato con la matematica statistica).